what statistical test to use to compare two percentages

An Introduction to T-Tests | Definitions, Formula and Examples

Published on Jan 31, 2020 past Rebecca Bevans. Revised on December 14, 2020.

A t-test is a statistical test that is used to compare the means of ii groups. Information technology is often used in hypothesis testing to decide whether a process or treatment actually has an consequence on the population of interest, or whether two groups are different from 1 another.

You desire to know whether the hateful petal length of iris flowers differs according to their species. You lot find two unlike species of irises growing in a garden and measure 25 petals of each species. You can exam the difference between these two groups using a t-test.

• The zippo hypothesis (H₀) is that the true deviation between these group means is null.
• The alternate hypothesis (H_a) is that the true departure is different from naught.

When to use a t-test

A t-test can simply exist used when comparing the ways of two groups (a.k.a. pairwise comparison). If you lot desire to compare more than two groups, or if you want to do multiple pairwise comparisons, use anANOVA test  or a mail service-hoc test.

The t-test is a parametric test of deviation, meaning that it makes the same assumptions about your data as other parametric tests. The t-test assumes your data:

1. are independent
2. are (approximately) normally distributed.
3. have a similar amount of variance within each group beingness compared (a.m.a. homogeneity of variance)

If your information do not fit these assumptions, you can try a nonparametric culling to the t-test, such equally the Wilcoxon Signed-Rank examination for data with unequal variances.

What type of t-test should I use?

When choosing a t-test, you volition need to consider two things: whether the groups being compared come up from a unmarried population or two different populations, and whether you desire to test the deviation in a specific management.

One-sample, ii-sample, or paired t-exam?

• If the groups come from a single population (eastward.one thousand. measuring before and later on an experimental treatment), perform a paired t-test.
• If the groups come from two different populations (e.1000. two different species, or people from two separate cities), perform a ii-sample t-exam (a.thousand.a. contained t-test).
• If there is one group beingness compared against a standard value (e.g. comparing the acidity of a liquid to a neutral pH of vii), perform a one-sample t-examination.

One-tailed or 2-tailed t-test?

• If y'all only care whether the 2 populations are different from one another, perform a two-tailed t-examination.
• If you desire to know whether i population mean is greater than or less than the other, perform a one-tailed t-test.

In your test of whether petal length differs by species:

• Your observations come up from ii split up populations (separate species), then y'all perform a ii-sample t-exam.
• You lot don't care about the direction of the difference, only whether in that location is a difference, so y'all choose to employ a 2-tailed t-test.

Performing a t-test

The t-test estimates the true divergence between two grouping means using the ratio of the departure in group means over the pooled standard mistake of both groups. Y'all can calculate it manually using a formula, or use statistical analysis software.

T-exam formula

The formula for the ii-sample t-test (a.k.a. the Student's t-examination) is shown below.

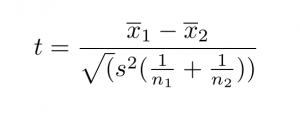
In this formula, t is the t-value, x ₁ and x ₂ are the means of the ii groups being compared, s ₂ is the pooled standard fault of the 2 groups, and due north _i and n ₂ are the number of observations in each of the groups.

A larger t-value shows that the deviation betwixt group ways is greater than the pooled standard error, indicating a more pregnant difference betwixt the groups.

You can compare your calculated t-value against the values in a disquisitional value nautical chart to determine whether your t-value is greater than what would be expected by adventure. If and so, you can reject the null hypothesis and conclude that the two groups are in fact different.

T-test role in statistical software

Most statistical software (R, SPSS, etc.) includes a t-test function. This born part will have your raw data and calculate the t-value. Information technology will then compare it to the critical value, and calculate a p-value. This style you lot tin quickly see whether your groups are statistically different.

In your comparison of flower petal lengths, you decide to perform your t-test using R. The code looks like this:

t.test(Petal.Length ~ Species, data = bloom.data)

Download the data set to practice by yourself.

Sample data set

Interpreting examination results

If you perform the t-exam for your flower hypothesis in R, you lot will receive the following output:

The output provides:

1. An explanation of what is existence compared, chosen data in the output tabular array.
2. The t-value: -33.719. Note that it'due south negative; this is fine! In most cases, we only care about the absolute value of the deviation, or the distance from 0. It doesn't thing which management.
3. The degrees of freedom: thirty.196. Degrees of freedom is related to your sample size, and shows how many 'free' data points are available in your test for making comparisons. The greater the degrees of freedom, the better your statistical test will piece of work.
4. The p-value: 2.2e-16 (i.e. 2.ii with 15 zeros in front end). This describes the probability that you would see a t-value equally large every bit this i by gamble.
5. A statement of the alternating hypothesis (H_a). In this test, the H_a is that the divergence is not 0.
6. The 95% confidence interval. This is the range of numbers within which the true difference in means will be 95% of the time. This tin can be changed from 95% if y'all want a larger or smaller interval, but 95% is very commonly used.
7. The hateful petal length for each grouping.

From the output tabular array, we can see that the difference in ways for our sample data is -4.084 (i.456 – 5.540), and the confidence interval shows that the true difference in means is betwixt -three.836 and -4.331. So, 95% of the fourth dimension, the truthful difference in means will be different from 0. Our p-value of 2.2e-16 is much smaller than 0.05, and so we can reject the nothing hypothesis of no difference and say with a loftier caste of confidence that the truthful deviation in means is not equal to cypher.

Presenting the results of a t-test

When reporting your t-examination results, the most important values to include are the t-value, the p-value, and the degrees of liberty for the test. These will communicate to your audience whether the departure betwixt the 2 groups is statistically significant (a.k.a. that it is unlikely to accept happened by chance).

You tin also include the summary statistics for the groups beingness compared, namely the mean and standard departure. In R, the code for calculating the hateful and the standard divergence from the data looks like this:

blossom.information %>%
group_by(Species) %>%
summarize(mean_length = mean(Petal.Length),
sd_length = sd(Petal.Length))

In our case, y'all would study the results like this:

The divergence in petal length between iris species 1 (Mean = i.46; SD = 0.206) and iris species 2 (Mean = 5.54; SD = 0.569) was significant (t (30) = -33.7190; p < two.2e-16).

Often asked questions about t-tests

What does a t-test measure?

A t-examination measures the difference in group means divided by the pooled standard error of the two group means.

In this way, it calculates a number (the t-value) illustrating the magnitude of the difference between the two group means being compared, and estimates the likelihood that this difference exists purely past take chances (p-value).

Which t-test should I use?

Your choice of t-exam depends on whether you are studying one grouping or 2 groups, and whether you intendance about the direction of the difference in grouping means.

If you are studying one group, utilise a paired t-test to compare the group mean over time or afterward an intervention, or use a i-sample t-test to compare the grouping hateful to a standard value. If you are studying 2 groups, use a 2-sample t-examination.

If you want to know only whether a difference exists, use a 2-tailed exam. If you desire to know if one grouping mean is greater or less than the other, utilize a left-tailed or right-tailed one-tailed examination.

What is the difference betwixt a ane-sample t-test and a paired t-test?

A one-sample t-test is used to compare a single population to a standard value (for example, to determine whether the average lifespan of a specific town is different from the state average).

A paired t-exam is used to compare a single population before and afterward some experimental intervention or at two different points in time (for case, measuring student operation on a test before and afterward being taught the material).

Is this article helpful?

You lot have already voted. Thanks :-) Your vote is saved :-) Processing your vote...

jonesplor1963.blogspot.com

Source: https://www.scribbr.com/statistics/t-test/

Share this post